3 main types of Design of Experiments (DOE) designs

Space fills. Fractional factorials. Full factorials. Optimal designs. Design of Experiments (DOE) offers a daunting compilation of types of design. As a beginner, understanding which one is right for your needs can feel like an impossible task.

To help you make the right choice, we’ll walk you through: 

• What to bear in mind when choosing a DOE design
• 3 main types of DOE designs that all beginners should know about, plus when and how to use them in your DOE campaign

Need a quick primer on DOE before we get started?

• What is Design of Experiments (DOE)?
• Why should I use Design of Experiments in the Life Sciences?
• The DOE process: A step-by-step guide

Choosing the right DOE design: What you need to know

There are just a few basic types, but lots of variations

The number of possible designs on offer can sometimes seem a bit overwhelming. 

Luckily, most fall into a few basic categories of design—or families, if you will.

The thing that defines these families is the DOE stage they’re most useful for. 

Stay with us and we’ll explain how the DOE stage is crucial for narrowing down which design you choose, and we’ll go through these basic categories in detail.

There’s also a whole other way of doing designs, where you use software to create a bespoke design to your exact requirements. These are called optimal designs, and it’s a topic for another day. 

A single DOE design type may not cover your whole DOE campaign

DOE’s repeated iterations means that you learn as you go. They can move you rapidly from your initial “thought experiment” to optimized conditions and robust data. 

Which means that you don’t have to design a single experiment—or pick a single DOE design—that will answer all your questions. DOE is best used sequentially. Each iteration should take you closer to your goal. 

DOE designs are suited to different stages of the DOE process

Instead of trying to fit your DOE campaign into a single experiment, think of the DOE process as a collection of sub-experiments. And for each sub-experiment, you might use a different design—as every type of DOE design at each step is intimately linked to a phase in the DOE campaign. 

This means that the goal per DOE campaign stage should guide your choice of design:

1. For the screening stage, you’ll need a design to help identify important factors and interactions.
2. For the refinement and iteration stage, you’ll need a design to help search for the optimum value in the potential range of factors.
3. For the optimization stage, you’ll need a design to help create a high-quality predictive model to infer optimal conditions.
4. For assessing robustness, you’ll need a design to help determine the extent to which the system is sensitive to changes in your factor levels.

Some DOE designs lend themselves to achieving the goals of more than 1 stage at a time, such as screening and optimization. Often, however, this isn’t possible. The choice depends on your factors and the system’s complexity. 

The design you choose will inform your analysis

Too often, analysis is an afterthought. You can spend ages trying to figure out which model fits.

The beauty of DOE is that by choosing a DOE design, you have also chosen the type of analysis you will do. By picking the right design in the beginning, you’ll be saving yourself tons of work and grief when it comes to the analysis.

Designs for later stages involve making trade-offs

As your campaign progresses, the DOE design types involve investing more experimental effort to answer more detailed questions. So, you may have to leave some things for later. You need to make a choice. 

Do you need an answer now? Can you do a couple of iterations? Some DOE designs allow you to compress some stages. But of course, this results in trade-offs and limitations. Though you’ll find that DOE software will often prevent you from making certain choices that your design does not permit.

3 main types of DOE designs, explained

At any stage in your DOE campaign, you could take your pick from several designs, depending on your assumptions, goals, available run numbers, and so on. 

But when you’re new to DOE, there’s nothing worse than having too many choices. Instead of covering all the designs in detail, we’ll start you off by covering the most commonly used and important DOE designs (Figure 1).

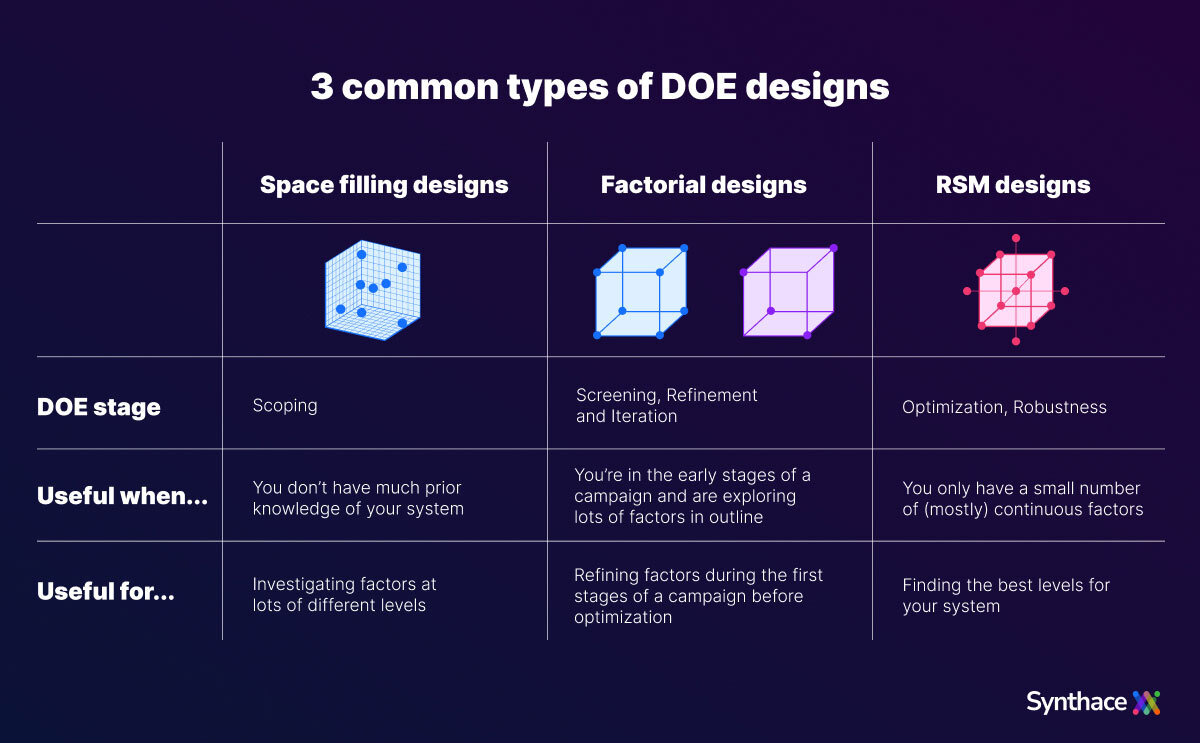
Figure 1: Common types of DOE design, the stage they’re linked to, plus when they are most useful

1. Space filling designs

DOE stage they’re linked to: Scoping

When to use them: Space filling designs are useful if you do not have much prior knowledge of your system, you want to investigate the system more broadly, or find a starting point for future optimization during pre-screening.

What they’re useful for: Space filling designs investigate factors at many different levels, without making any assumptions about the structure of the space, or the type of model. This means that you lose the efficiency and some statistical properties of classical DOE designs, such as factorials. 

2. Factorial designs

DOE stages they’re linked to: Screening, Refinement and Iteration

When to use them: You typically use factorial designs in the early stages of a DOE campaign: Screening, plus iteration and refinement. They’re helpful when you’re exploring a lot of factors in outline.

What they’re useful for: You can use factorial designs with any type of factor. Though it’s worth keeping the number of levels small so you can explore more factors. With continuous factors, for example, you’d normally stick to 2 levels, representing the maximum and minimum of an interval of interest. 

Single central points in factorial designs

Many factorial designs add a single central point for each factor to help determine whether there is curvature. This can help you better understand the experimental space.

For example, imagine that we’re growing a crop of strawberries. By adding a single central point, it can guide you to the best (mean) yield, rather than an incorrect one (Figure 2). 

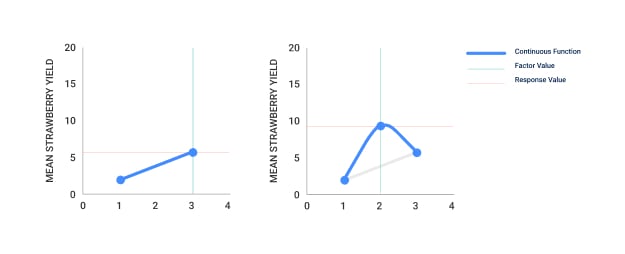Figure 2: The value of adding a single central point can guide you to the actual local maxima rather than an incorrect one

Full factorial vs fractional factorial designs

There are also two main types of factorial design: Full and fractional. 

Full factorial designs

Full factorial designs investigate all possible combinations of factors and levels. So, you can determine main effects and any order of interaction. Full factorial designs, however, involve a large number of runs, increasing exponentially as the number of factors increase. 

Full factorial designs are often most appropriate when screening has identified a few important factors to optimize, or when using liquid handling automation affording an increase in throughput. 

Look to Figure 3 for an example in action: It shows how a full factorial works through every combination of every factor that screening suggested could influence the yield of strawberries. 

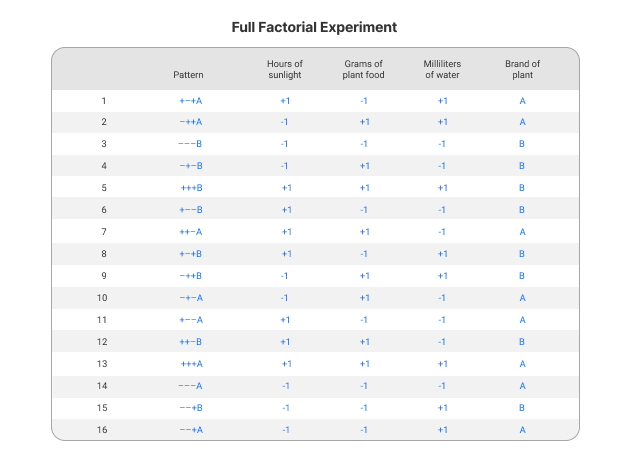
Figure 3: A full factorial design to uncover the best conditions for yield in a strawberry crop

Fractional factorial designs

When factors or levels increase, full factorial designs can become infeasible—even in sophisticated, high-capacity facilities. You can use fractional factorial designs when you have a large number of factors to screen, or where resources are limited.

A fractional factorial design takes a rational sample of the experimental landscape to provide a balanced, structured design that generates explanatory and predictive models. 

Fractional factorial designs assume that while there may be many effects, only a few are important. They also assume that the lower order effect. In other words, interactions between 2 factors—are more common and more influential than higher order effects (typically, interactions between more than 3 factors). 

So, the design doesn’t include the high-order interactions with each other, which drastically reduces run numbers. 

Fractional factorial DOE is not, however, suitable for sophisticated modeling. 

Let’s use growing strawberries as our example: Figure 4 shows how a fractional factorial design still covers a lot of ground in only half the runs, which saves time and resources.

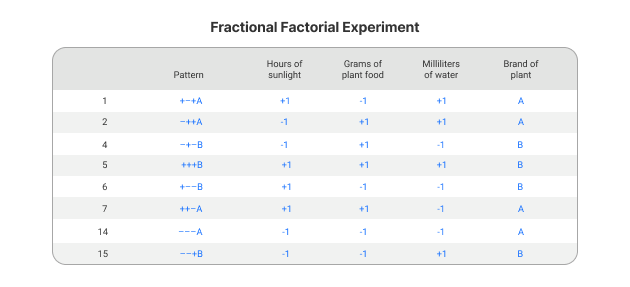
Figure 4: A fractional factorial design for growing the yield of the same strawberry crop

Assessing fractional factorial designs with aliasing in mind

Every run is required to distinguish some combination of factors. So naturally, by taking runs out of a factorial, as you would with fractional factorials, you inevitably end up aliasing between 2 effects. Translation: The 2 effects cannot be distinguished from each other.

Aliasing forms the foundation of fractional factorial designs—and it’s something that you have to bear in mind when assessing them. When analyzing data you can encounter a situation where you can’t tell whether, for example, an interaction between 2 or 3 factors causes a particular effect. You either have to use your existing knowledge to decide or, if necessary, do more experiments.

Aliasing is particularly useful during screening to explore more factors without incurring a huge experimental cost. If you assume that higher order effects are likely to be less important than lower order effects (main effects and interactions between 2 factors), then you can alias higher order interactions with each other and substantially reduce the number of runs. 

Ultimately, assessing a particular fractional factorial is about deciding whether you can determine any of the particular higher order effects that you think might be interesting.

Assessing factorial designs with power and resolution

When you’re assessing your design, it’s important to think about power: Your ability to tell any effects apart from random noise.

It’s also important to think about resolution. 

Imagine that you’re looking at a high-resolution picture. It’s so clear, it’s easy to distinguish pixels that are sitting next to each other. Now, imagine you're looking at the same picture with a much lower resolution. It’s grainy, and it’s impossible to identify one pixel from the next. 

The same problems of having “low resolution” will apply to your DOE design. As when it comes to fitting a model to your data, if your DOE has a really low resolution, you won’t be able to tell the difference between effect a) and effect b). Whereas if you have a “high resolution”, distinguishing between one effect and another is easy. In short, resolution is all about assessing your design by how well you can tell different effects apart. 

You normally “grade” resolution with a number. This number tells you what “order”—or in non “DOE speak”, the size—of interactions you can distinguish within a particular effect. In other words, whether you can tell one 2-factor from another 2-factor interaction. 

3. Response surface methodology (RSM) designs

DOE stage they’re linked to: Optimization, Robustness

When to use them: Typically best for the optimization and robustness stages, you can use Response surface methodology (RSM) designs, also called specific names, such as Box-Behnken or central composite designs, if you detect significant factors during screening that display curvature (Figure 2).

In reality, there are nuances to the different types of RSM designs. Though some types of RSM designs can be thought of as full factorial designs across 2 levels for each factor, with center and axial points to sample additional levels without needing to do a full factorial across all levels. 

So, if you used a 2-level full factorial design during the refinement and iteration stage, you only need to add the axial points and replicated center points to achieve an RSM design.

This translates into a small amount of additional experimental work and can be a useful pattern when iterating from stage to stage of your DOE campaign. 

What they’re useful for: RSM designs can be applied to many kinds of factors. In general, however, RSM designs are not applied to categorical and discrete factors, as the experimental effort, or in other words, the number of runs you need, can become very expensive.

Optimizing your response with RSM designs

RSM designs allow you to build a predictive model of your system’s response surface. You can then use the predictive model to find the factor settings or region that will optimize your response. 

Check out Figure 5: If your design space is a mountain, the optimum response may be the peak. You are searching for the ideal convergence of factors that shows us where the peak is on this particular topographical map. 

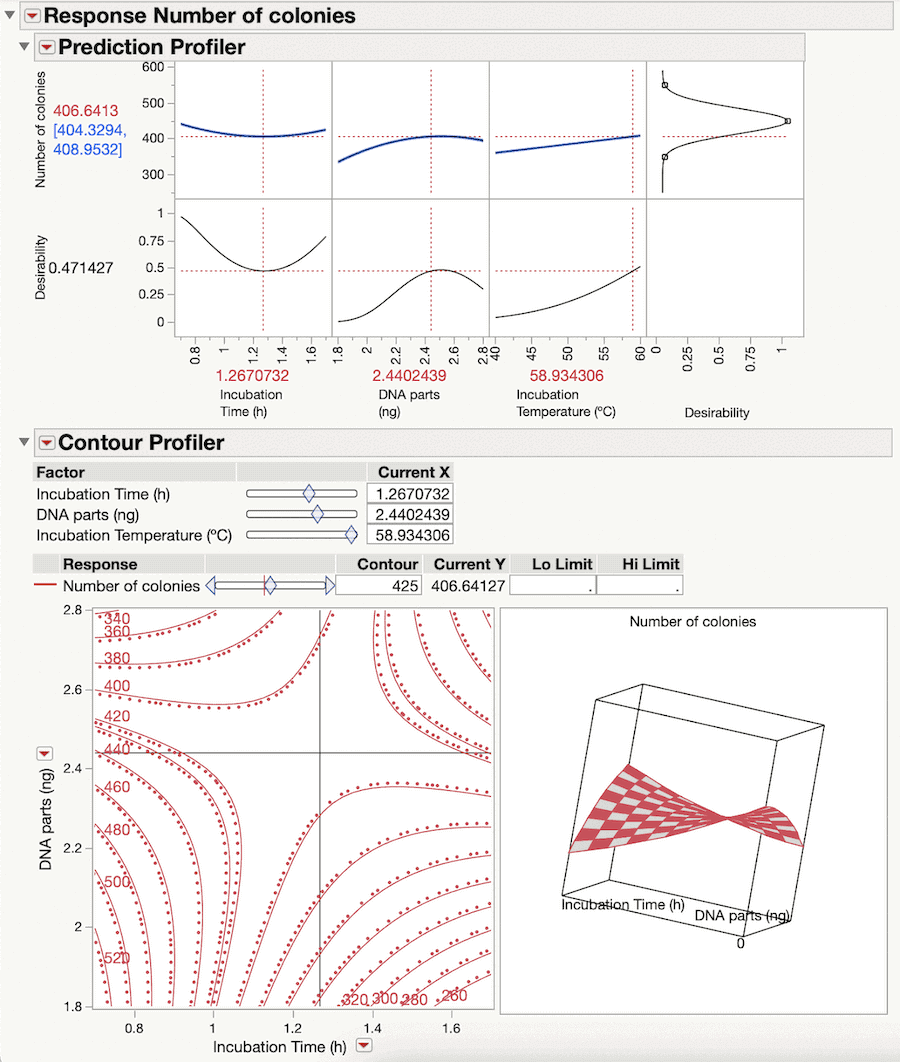
Figure 5: Response surface methodology

RSM designs share many features with factorial designs. The assessment, however, differs. Instead of concepts like power and aliasing, which are relevant to determining which effects are real, RSM uses concepts relating to the errors when making predictions in the relevant design space. 

Pick the right design, unleash the power of DOE

It’s easy to get overwhelmed by all the design choices that most DOE software gives you. Most DOE software, especially our own, is also there to help guide you. They can also help you identify when technical restrictions apply and avoid making the wrong choice. 

And when in doubt? Remember to let your DOE campaign stage guide your design choices. It can also be helpful to think about how much work you can actually do—and find a design that fits your budget. Typically, if you have an unmanageable number of runs, you’ve likely picked the wrong design. 

And if you’re still in doubt? Remember that picking a design is better than no design! You’ve got to start somewhere.

This was an adaptation of a section from our DOE ebook: a biologist’s guide to Design of Experiments. Download it for free!

Dive deeper into Design of Experiments:

• Sign up for our free DOE training course to learn the fundamentals in 6 minutes a day 
• Watch our DOE Masterclass webinar series
• Get our top 7 DOE books worth reading in 2024